Table of Contents
- Background
- N Queens Revisited
- Perl Solution
- Python Solution
- Python vs. Perl: Walltime vs. Number of Queens
- Perl Profiling and Results
- Python Profiling
- Python Profiling Results
- Comparing Python to Perl
- Python vs. Perl: Walltime vs. Number of Solutions Tested
- The Winner: Perl for Small Problems, Python for Big Ones
- Sources
Background
Revisiting the N queens problem, this time implementing the solution in Python.
Verb-oriented solution, functional, and based on Perl solution
More fair comparison - both are interpreted languages, not compiled languages
Compare Python and Perl, ease of implementation, speed, flexibility
N Queens Problem
As a recap from the last post about the N queens problem, we're solving a chess puzzle that asks: how many different configurations are there for placing \(N\) queens on an \(N \times N\) chessboard such that no queen attacks any other queen?
This is a popular problem in computer science because solutions often implement recursive backtracking.
See the Wikipedia article for details.
N Queens Solution
Here is the pseudocode of the N queens solution being implemented here:
explore(column):
if last column:
# base case
add to solutions
else:
# recursive case
for each row:
if this is a safe row:
place queen on this row
explore(column+1)
remove queen from this row
This solution implements recursive backtracking to explore choices of where to place each queen. It keeps solutions simple, and can be implemented using only primitive built-in data types. Solutions are stringified version of these arrays, consisting of 8 digits, so they are likewise very simple.
Perl Solution
As a reminder, the Perl solution was originally from Rosetta Code. Here's another link to the Perl solution on Github.
Python Solution
The solution requires the use of one array of data that is fixed in size, which for a given column stores a list of rows already occupied by queens, and one array of data that is variable in size, which stores where each queen has been placed.
The Python solution makes use of lists by using a fixed-size list for the occupied rows and a variable size list for storing queen locations. It utilizes buit-in methods for the list data type to append and pop, or add and remove items from the end of the list.
Head to Head: Walltime vs. Number of Queens
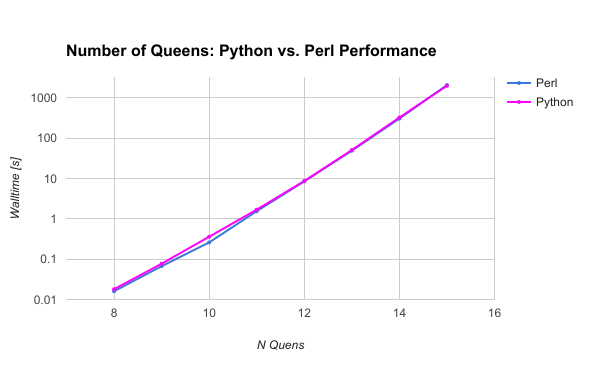
----------------------------------------------------------
| NQueens | Nsolutions | Java | Perl | Python |
|---------|------------|-----------|----------|----------|
| 8 | 92 | 0.003628 | 0.016 | 0.018 |
| 9 | 352 | 0.006709 | 0.067 | 0.077 |
| 10 | 724 | 0.017473 | 0.259 | 0.359 |
| 11 | 2680 | 0.061291 | 1.542 | 1.684 |
| 12 | 14200 | 0.240463 | 8.431 | 8.618 |
| 13 | 73712 | 1.113491 | 48.542 | 50.401 |
| 14 | 365596 | 6.557336 | 303.278 | 322.576 |
| 15 | 2279184 | 42.619426 | 2057.052 | 1979.343 |
----------------------------------------------------------
The results of this test show that Python and Perl are fairly closely matched.
Perl Profiling
Results of profiling the Perl code with Devel::NYTProf were detailed in a prior post.
Here are those results once again, for the 11 queens problem:
# Profile data generated by Devel::NYTProf::Reader
# Version: v6.04
# More information at http://metacpan.org/release/Devel-NYTProf/
# Format: time,calls,time/call,code
0.000238,2,0.000119,use Time::HiRes qw(time);
0.000039,2,0.000019,use strict;
0.000491,2,0.000246,use warnings;
0.000021,1,0.000021,my $start = time;
0.010338,2680,0.000004,push @solutions, "@queens\n";
0.009993,2680,0.000004,return;
0.186298,164246,0.000001,$#attacked = 2 * $board_size;
0.150338,164246,0.000001,for( 0 .. $#queens) {
0.675523,1.26035e+06,0.000001,$attacked[ $ix2 ] = 1;
1.242624,164246,0.000008,for my $row (0 .. $board_size-1) {
0.267469,166925,0.000002,explore($depth+1);
0.125272,166925,0.000001,$occupied[$row] = 0;
0.000002,1,0.000002,explore(0);
0.000011,1,0.000011,my $duration = time - $start;
0.000075,1,0.000075,print "Found ", scalar(@solutions), " solutions\n";
0.000050,1,0.000050,printf "Execution time: %0.3f s \n",$duration;
Python Profiling
The Python N queens solution was profiled with two tools: cProfile and line_profiler.
The built-in profiling tool cProfile gives a summary of how much time was spent in each method,
but nothing lower level than that. It is similar to Java profiling tools. (cProfile documentation)
The line_profiler tool is designed to profile Python code line-by-line, which gives a much more useful
breakdown of where the code spent all of its time. It is also helpful because this can be compared one-to-one
with the results from Perl, and we can get an equal basis for comparing the two languages.
Python Profiling Results
cProfile Results
Here are the results from running the N queens problem for N = 11 through cProfile:
**************************************
Profiling 11 queens problem with Python...
*******************************
cProfile:
*******************************
Found 2680 solutions
996197 function calls (829272 primitive calls) in 2.237 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
166926/1 1.845 0.000 2.237 2.237 /Volumes/noospace/Users/charles/codes/hello-world/python/nqueens/nqueens.py:12(explore)
328492 0.275 0.000 0.275 0.000 {range}
166925 0.062 0.000 0.062 0.000 {method 'pop' of 'list' objects}
169605 0.029 0.000 0.029 0.000 {method 'append' of 'list' objects}
164247 0.026 0.000 0.026 0.000 {len}
1 0.000 0.000 2.237 2.237 /Volumes/noospace/Users/charles/codes/hello-world/python/nqueens/nqueens.py:4(<module>)
1 0.000 0.000 0.000 0.000 {method 'disable' of '_lsprof.Profiler' objects}
line_profiler Results
The line_profiler tool gives a more detailed picture of the code and where it spends its time,
breaking down profiling information line-by-line. This tool can be installed with pip: pip install line_profiler.
The (INSERT LINK)(nqueens repository on github) has a file that demonstrates how to use this tool.
See Python/Profiling
Here are the results from the line_profiler tool run on the same (11 queens) problem:
**************************************
Profiling 11 queens problem with Python...
Found 2680 solutions
Wrote profile results to nqueens.py.lprof
Timer unit: 1e-06 s
Total time: 14.2258 s
File: nqueens.py
Function: explore at line 11
Line # Hits Time Per Hit % Time Line Contents
==============================================================
11 @profile
12 def explore(depth):
13 # base case
14 166926 187573 1.1 1.3 if(depth==board_size):
15 # stringify/serialize the solution
16 2680 31497 11.8 0.2 solutions.append("%s"%(queens))
17 2680 3117 1.2 0.0 return
18
19 else:
20 164246 384688 2.3 2.7 attacked = 2*board_size*[0,]
21 1424595 1690693 1.2 11.9 for i in range(0,len(queens)):
22 1260349 1471304 1.2 10.3 ix1 = queens[i] + depth - i
23 1260349 1405141 1.1 9.9 attacked[ix1] = 1
24
25 1260349 1494095 1.2 10.5 ix2 = queens[i] - depth + i
26 1260349 1392563 1.1 9.8 attacked[ix2] = 1
27
28 1970952 2229922 1.1 15.7 for row in range(0,board_size):
29 1806706 2031139 1.1 14.3 if(occupied[row] or attacked[row]):
30 379432 374466 1.0 2.6 continue
31
32 # make a choice
33 166925 241114 1.4 1.7 queens.append(row)
34 166925 186833 1.1 1.3 occupied[row] = 1
35
36 # explore the consequences
37 166925 610396 3.7 4.3 explore(depth+1)
38
39 # unmake the choice
40 166925 288667 1.7 2.0 queens.pop()
41 166925 202555 1.2 1.4 occupied[row] = 0
Python vs Perl: Walltime vs. Number of Solutions Tested
As with the prior post, I verified that both codes were testing the same number of solutions. Here is that table of the number of solutions for each value of N, together with the number of solutions tested:
-----------------------------------------------------------------------------
| NQueens | Nsolutions | NsolutionsTested | Java | Perl | Python |
|---------|------------|------------------|-----------|----------|----------|
| 8 | 92 | 1965 | 0.003628 | 0.016 | 0.018 |
| 9 | 352 | 8042 | 0.006709 | 0.067 | 0.077 |
| 10 | 724 | 34815 | 0.017473 | 0.259 | 0.359 |
| 11 | 2680 | 164246 | 0.061291 | 1.542 | 1.684 |
| 12 | 14200 | 841989 | 0.240463 | 8.431 | 8.618 |
| 13 | 73712 | 4601178 | 1.113491 | 48.542 | 50.401 |
| 14 | 365596 | 26992957 | 6.557336 | 303.278 | 322.576 |
| 15 | 2279184 | 168849888 | 42.619426 | 2057.052 | 1979.343 |
-----------------------------------------------------------------------------
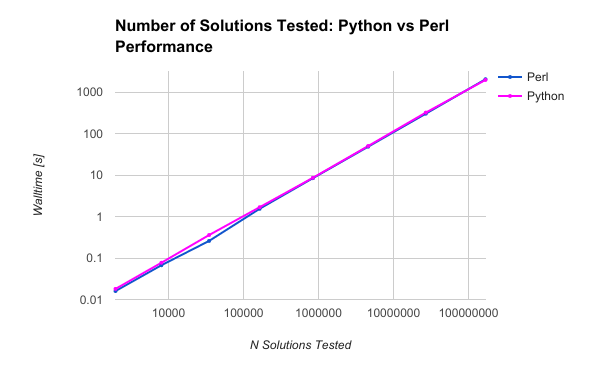
The Winner: Perl for Small Problems, Python for Big Ones
It was not a big surprise to see that Perl and Python were nearly identical in their performance, and it testament to the fact that interpreted scripting languages like Perl and Python operate at one speed, and compiled code in C++ or Java operates at a completely different speed that is an order of magnitude faster (see the comparison of Perl and Java in a prior blog post).
Perl and Python were close enough in performance that, although Perl came out ahead on smaller problems and Python came out ahead on the biggest, a different CPU or platform, micro-optimizations, and various butterfly effects could easily turn the tables.
Sources
-
"N-Queens Problem". Rosetta Code, GNU Free Documentation License. Edited 6 March 2017. Accessed 21 March 2017. <https://web.archive.org/web/20170320081421/http://rosettacode.org/wiki/N-queens_problem>
-
"nqueens.py". Charles Reid. Github Gist, Github Inc. Edited 25 March 2017. Accessed 25 March 2017. <https://gist.github.com/charlesreid1/1a2ecb3a83284290d4a9daf747d0d7e4>
-
"nqueens.pl". Charles Reid. Github Gist, Github Inc. Edited 20 March 2017. Accessed 23 March 2017. <https://gist.github.com/charlesreid1/4ce97a5f896ff1c89855a5d038d51535>
-
"The Python Profilers". Python 2.7.13 Documentation, Python Software Foundation. Updated 20 February 2017. Accessed 23 March 2017. <https://docs.python.org/2/library/profile.html>
-
"line_profiler". Python Package Index, Python Software Foundation. Updated 20 October 2016. Accessed 23 March 2017. <https://pypi.python.org/pypi/line_profiler/>
-
"Github - rkern/line_profiler". rkern, Github Repository, Github Inc. Updated 20 October 2016. Accessed 23 March 2017. <https://github.com/rkern/line_profiler>
-
"Python/Profiling". Charlesreid1.com wiki, Charles Reid. Edited 23 March 2017. Accessed 23 March 2017. <https://web.archive.org/web/20170326031708/http://charlesreid1.com/wiki/Python/Profiling>