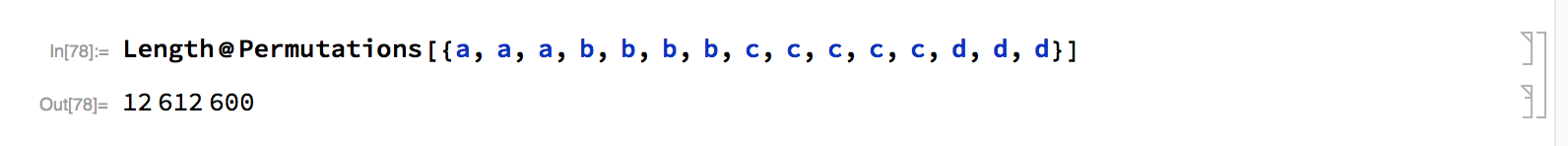The Lattice Paths Problem
I first came across the lattice paths problem in Project Euler problem 15. The question described a 2x2 square lattice, and illustrated the 6 ways of navigating from the top left corner to the bottom right corner by taking the minimum number of steps - 2 right steps and 2 down steps.
The question then asks for the number of minimum paths on a 20 x 20 grid. Needless to say, even without seeing the number, it should be obvious that enumerating all of these paths would get extremely expensive with grid dimensions growing beyond 10. That means this should be approached as an analytical combinatorics problem, not a computational combinatorics problem. As it turns out, there is a closed-form solution, and this is one of the few Project Euler questions that can be answered with the straightforward use of Wolfram Alpha (I solved it while boarding a bus).
But this is an interesting problem that goes beyond the Project Euler question - it has to do with a combinatorics problem that is maddeningly simple, yet surprisingly difficult to formulate - the problem of multisets.
Problem Formulation: Permutations
Thinking through the 2x2 grid, we already stated that the shortest path must consist of 2 right moves and 2 down moves - the number of paths is simply a question of the order in which these moves are made. Let us represent the path that moves right twice, then down twice, using the string
RRDD
Now we have a way of representing paths through the lattice - and we've turned our very specific lattice problem into a much more general combinatorics problem. How many unique permutations of the above path/string can we find?
Permutations of Unique Items (Factorial)
Let's suppose we have a string consisting of unique characters:
ABCDEFG
Now how many permutations of this string are there? The first letter can be any of the 7 characters, so we have 7 possibilities. The second letter can be any of the remaining 6 characters, so we have 7 * 6 possibilities. And so on down the line, until we get a total number of possible permutations of the string equal to
There are 5040 unique permutations of the string.
Our situation is complicated by the fact that some of our permutations are repeated. For example, if we label the two down moves as D1 and D2, we can choose the first move as D1 and the second move as D2, or the first move as D2 and the second move as D1 - the two are equivalent. This will eliminate some of the permutations.
Permutations of Items with Duplicates (Multichoose)
Our case is slightly different: we have items with duplicates. This fits into a general combinatorics framework called stars-and-bars (link to Wikipedia article). In this framework, we are trying to determine the number of ways that we can partition a set of n objects into a set of \(k\) bins. The \(n\) objects are often denoted as star characters, and the k bins are formed by k-1 bar characters.
For example, if we are adding 5 components to a circuit board, and they can be any one of 9 possible components, we can represent this as the partitioning of 5 stars among 9 bins, or 8 bars. Here are some possibilities:
|||||||| <-- No choices made yet (9 bins, 8 partitions)
*|*||*||*|*|| <-- Mix of different components
||*|*||*|*||* <-- Mix of different components
****|||*||||| <-- Heavy on component 1
*|**|||**|||| <-- Two pairs
In the case of our lattice path problem, we have only two unique characters, D and R. We can think of the problem of generating permutations as inserting the down moves into a sequence of right moves. We have a certain number of locations where we can insert the down moves, and down moves can be inserted in order.
This is what's often called a stars-and-bars problem in combinatorics: trying to determine the number of permutations of items from multisets can be described as partitioning star characters with bar characters.
To formulate our problem in these terms, we can think of "distributing" our down moves as we move right through the lattice. On the 20x20 grid, we are going to make 20 right moves, and we can distribute our 20 down moves at any of 21 possible locations (columns of points on the lattice).
Thus, our n items, the 20 down moves, are being placed between the 20 right moves, which are the 20 bars that create 21 bins (21 locations to place the down moves).
Example
Considering the smaller 2x2 example, and replacing bars with R, we have, for a 2x2 lattice, six possibilities:
RR <-- No choices made yet
**RR <-- all on left
*R*R <-- distributed... etc...
*RR*
R**R
R*R*
RR**
To enumerate the number of possibilities, we use the multichoose function, denoted "n multichoose k". This counts the number of ways to place n objects (D) into \(k\) bins (created by \(k-1\) other objects, R). The multichoose function is defined as (see https://en.wikipedia.org/wiki/Multiset#Counting_multisets Wikipedia page for proper Latex notation - it looks like the binomial coefficient but with 2 parentheses):
where, again, n is number of objects, being split into \(k\) partitions by \(k-1\) other objects.
Now, let's plug in the numbers for the 2 by 2 lattice. We get:
We are partitioning 2 down moves among 3 possible columns in the lattice. This gives:
which is indeed the number of paths through the lattice.
Solving 2D Rectangular Lattice
To generalize, on a lattice of width \(W\) and height \(H\), we have \(W\) right moves that form \(W+1\) partitions, in which we are placing H items. The number of possible paths through the lattice is therefore equivalent to permutations of the string:
RRRR...(W times)...RRRDDDD...(H times)...DDDD
Now n and k are given by:
so the total number of possible paths through the W x H square lattice is:
More Examples
The number of minimal paths through a 4 x 2 lattice (identical to the number of paths through a 2 x 4 lattice) is:
The number of minimal paths through an 8x8 lattice is given by:
and finally, the number of minimal paths through a 20 x 20 lattice is given by:
(This is the Project Euler problem 15 answer so last few digits are omitted.)
Solving 2D Square Lattice (Special Case)
If we use the above formulas for the special case where the dimensions of the grid are equal, such as the 20 x 20 case, we get the simpler and more symmetric formula:
where \(D\) is the dimension of the square grid.
Solving 3D Cuboid Lattice
(Note: cuboids are the 3D analogue of 2D rectangles.)
If we take this idea a step further, and use a slightly different combinatoric formula, we can generalize the problem to paths through higher dimensional lattices. This is an approach I came up with through trial and error, and some experimentation with Mathematica.
Suppose we have a 3D lattice, composed of 8 cubes, 2 on each side. Now we wish to know: how many shortest Manhattan distance paths are there through the lattice, from one corner to the other?
This can be re-cast, as we did above, as the problem of counting unique permutations of a string of the form:
UURRBB
where U denotes an up move, R denotes a right move, and B denotes a back move.
While we could use the multiset approach from above to describe this problem, it turns out that this approach is not powerful enough to describe the problem of arbitrary 3D lattices.
Let's pose the problem slightly more generally: we have C bags of moves or characters, each of a different size. We must use each character i precisely as many times as we have instances in its bag C_i. How many unique permutations are there?
Consider the following example string of length \(N = 14\), consisting of:
These form a path through a 3D lattice of size \(4 \times 4 \times 6\):
UUUURRRRBBBBBB
The number of unique permutations can be computed by breaking this into sub-problems. Start by asking how many permutations there are of the string:
UUUUXXXXXXXXXX
(Treating the Rs and Bs as identical). Then we get:
Next, we deal with the other sub-problem, the Xs, by asking how many ways we can permute the following string:
RRRRBBBBBB
which is solved via another binomial coefficient. This number of permutations is given by:
Now combining these, we get the overall number of permutations:
Solving 3D Cubic Lattice (Special Case)
If we have the special case of a perfect cubic lattice, the formula above reduces to the nice and symmetric:
Solving N-Dimensional Square Lattice (N-Dimensional Multisets)
Let's look at the example of a traversal of a 4D lattice, which we can think of as the evolution of a 3D traversal in time (a step in the fourth dimension would represent a "pause" in the 3D traversal).
Consider the traversal of a cube with dimensions \(3 \times 4 \times 5 \times 3\). Then
A path on this 4D lattice has the form:
UUURRRRBBBBBWWW
(where \(W\) denotes wait, or a step in the time dimension).
The number of permutations is given by:
For our specific example,
Confirmed by Mathematica: