Table of Contents

• Intro
• Running with Gitea
  • Binary or Source
  • Configuring Gitea Directories
  • Opening the Firewall
  • Setting Up and Configuring Gitea Server
• How To Use Gitea
  • Pushing a Local Repo Into Gitea
  • Copying Repos from Github to Gitea
  • "Moving" Repos from Github to Gitea
  • Pushing Commits to Github or Gitea
  • Backing Up Gitea
• How Gitea Fits Into Git Patterns
• Wrapup

Intro

In this post we'll cover how to set up a web-hosted git server that uses Gitea, a Github clone that is written in Go. While this post is not, strictly speaking, research, having your own hosted git server certainly makes it easier to manage research codes and set up organizations to own different bits of code.

Here's an image of a git repository in the finished product:

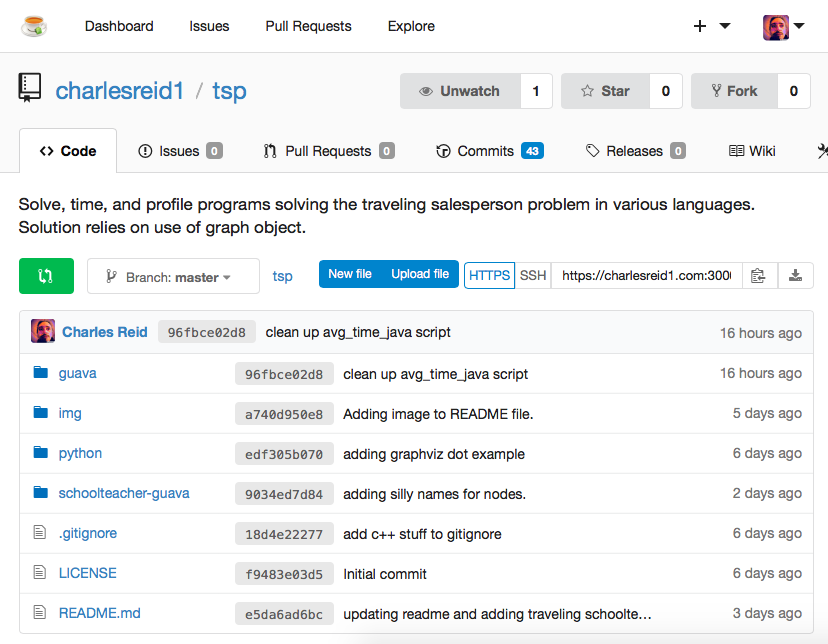
We will start by covering the server configuration for Gitea, and then we'll cover how to use Gitea's git repository.

Running with Gitea

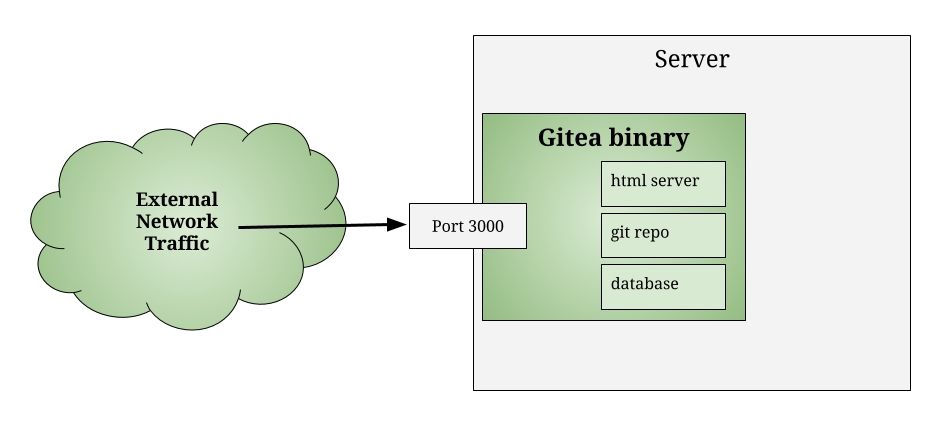
Gitea is a web app for running a self-hosted Github clone. It is implemented entirely in the Go language, so all of the pages that are served up are assembled by the Go binary. The Go binary also has a local instance of git running, and any actions taken through the Gitea web interface are translated, by the Go binary, into actions in the git reopsitory.

Out of the box, Gitea provides all of this functionality, and takes care of all the details, so you don't have to worry about any of this. But if you build it yourself, you can modify the content the binary serves up and the actions it takes.

In this guide, we'll stick to the binary.

Binary or Source

There are some problems with the source code that may make compilation from source impossible. (See charlesreid1.com wiki notes.) The binary version of Gitea is recommended.

Configuring Gitea Directories

Gitea expects a certain directory organization, specifically, a folder for binaries, certificates, a database, git repositories, and the log.

The recommended arrangment is:

/path/to/www/gitea/
   \
    \---------- bin/
     \--------- certs/
      \-------- data/
       \------- repositories/
        \------ log/

Once the files are organized in this way, navigate to the bin directory and (preferrably using tmux or screen to send to background) execute the command:

./gitea web

This runs a setup page on port 3000.

Note that you may or may not need to set your $GOPATH variable:

export GOPATH="${HOME}/gocode"

Go ahead and follow the instructions on the page to get Gitea set up. The gitea.io page has good documentation.

Opening the Firewall

Assuming your port 3000 was closed on the firewall, and assuming you plan to run the gitea service as a public service listening on an external port, you will want to open your firewall to accept incoming traffic on port 3000:

# allow traffic on port 3000
iptables -A INPUT -p tcp --dport 3000 -j ACCEPT
#  to allow forwarding for 3000 to internal LAN 
iptables -A FORWARD -p tcp -j ACCEPT --dport 3000 -m state --state NEW

Setting Up and Configuring Gitea Server

To configure gitea, you will use a .ini configuration file contained in:

/path/to/www/gitea/custom/conf/app.ini

Here is an example gitea configuration file. It starts with a header, then has sections for different aspects like databases, the git repository, and the server:

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;; Example Gitea Config File
;;
;; https://github.com/go-gitea/gitea/blob/master/conf/app.ini
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

APP_NAME = big ugly git repo (BUGR)
RUN_USER = git
RUN_MODE = prod

[database]
DB_TYPE  = sqlite3
SSL_MODE = disable
PATH     = /www/gitea/data/gitea.db

[repository]
ROOT = /www/gitea/repositories
PREFERRED_LICENSES = MIT License

[server]
PROTOCOL     = https
DOMAIN       = yourdomain.com
CERT_FILE    = /www/gitea/certs/cert.pem
KEY_FILE     = /www/gitea/certs/key.pem
SSH_DOMAIN   = git.yourdomain.com
HTTP_PORT    = 3000
ROOT_URL     = https://yourdomain.com:3000
DISABLE_SSH  = false
SSH_PORT     = 22
OFFLINE_MODE = false

[log]
ROOT_PATH = /www/gitea/log

Ultimately, there are many configuration examples available for Gitea, so we won't go into any more detail on that.

For details on how to configure Gitea with HTTPS, see charlesreid1.com/wiki/Gitea.

Let's move on to how we actually utilize Gitea, and focus especially on how to make gitea work in tandem with github and other git servers, instead of being yet another complication in the toolchain.

How To Use Gitea

As we mentioned before, the gitea binary is actually wrapping a git repo, and interactions with the binary (via the web) are translated into actions in that repo. This is important to understand, since it will prevent us from thinking about gitea as a "centralized" server, and get us thinking about gitea as just another computer with a copy of the repository on it.

Understanding how to use gitea also requires correct thinking about how distributed version control works - the way that each collaborator with a copy of the repo can also act as a decentralized git server. In this way, the gitea server becomes just another git client, with some extra frosting on top in the form of a web interface.

Pushing a Local Repo Into Gitea

If you want to move existing local repositories into gitea, it's easy. Remember that with git, everything is local, so all you need to do is push a copy to gitea, and gitea will have the whole repository locally too, including its entire history and any branches and tags that were on your local machine. If you have remotes, you'll need to get local copies of any branches or tags you want from that remote server (covered in more detail below).

The basic steps: * Get everything you want locally (including branches and tags) * Fetch from remotes, if you have any. * Add new remote (gitea) * Push to new remote

The end result will be a gitea repo fully-populated with the project's commit history.

Here are the steps in a bit more detail:

Start by creating a git repository, or cloning an existing one:

mkdir my_git_repo/
cd my_git_repo
git init .

or

git clone http://github.com/mot_pesli/coune_car

Next, create an empty git repo on the gitea server. Sign in using a gitea username and password. There will be a plus sign in the upper right, just like on Github. Click the plus sign, and choose create new repo. Enter the repo name, and a description. Make sure the repo will NOT automatically create a readme or a LICENSE file, as we will be importing all files from another repo anyway.

Once you've got a local copy of the repo with everything you want to push, and you have an empty repository on the gitea server ready for commits, add the gitea repository as a new remote to your local repository.

Example: suppose you have a gitea user named zappa who has created a new empty repo named linol-aquabus on the gitea server. Zappa would then cd to the local copy of the git repo, and add the gitea repository's url as a new remote called gitea:

git remote add gitea https://git.mydomain.com/zappa/linol-aquabus.git

# alternatively,

git remote add gitea https://mydomain.com:3000/zappa/linol-aquabus.git

Now Zappa can push the entire commit history of the current repo to the gitea remote git server:

git push origin gitea

# alternatively,

git push --all origin gitea

If Zappa now visits mydomain.com:3000/zappa/linol-aquabus the entire contents of the repository and its commit history in gitea's web interface will be available for browsing.

Copying Repos from Gitub to Gitea

The process for copying Github repositories to Gitea follows the above procedure closely:

git clone https://github.com/user/repo.git

Check out any branches or tags you may want to push to gitea.

Then add the gitea remote to the repo:

git remote add gitea https://git.mydomain.com/zappa/linol-aquabus.git

Now push the contents of the local repository to the remote gitea repository:

git push origin gitea

Once this command is executed, the gitea remote will have the entire commit history of the repo, which it will render and display through its web interface. Thus, the entire commit history will be immediately available to browse through gitea.

(Note that information about Github issues or Github user profiles is not stored in the git repo, just as Gitea comments and Gitea user profiles are not stored in the git repo.)

"Moving" Repos from Gitub to Gitea

First, it should be stated up front that you do not have to choose between gitea and github - you can have a copy of a repo on both, frequently push to one or the other, and occasionally update the other as a kind of "mirror."

If you do want to move a repo from github to gitea, remember that github does not "own" the repo, so what you're actually doing is deleting the copy of your repo that lives on github's server.

To move the repo, all you have to do is copy it from github to somewhere else (whether it be your local computer, or to the gitea server), then delete it from github. You will not lose any information about the git repository history. Github does not keep/store that information - git does.

Where to Push Commits: Github or Gitea?

It may seem confusing to use multiple repositories side-by-side, but this is precisely how the designers of git intended it to be used - for decentralized version control.

That means Github or Gitea are not "centralized" servers that "own" the repository, they are merely another instance of git, running on a server, with a local copy of the repo.

Accordingly, if your project exists as a repo on gitea and as a repo on github, it is like the project existing as a repo on your hard drive and as a repo on your collaborator's hard drive - there is no contradiction. If you make changes to your local copy of the repo, you can commit those changes, then push the commits to someone else. In the same way, you can make changes to your local copy of the repo and commit those changes, then push the commits to either gitea, or github, or both - wherever you want.

Backing Up Gitea

It's important to say a few words about backups.

Because Gitea is configured (with the above config file) to use sqlite, it stores its entire database (the extra "frosting" of stars, wiki pages, issues, user pictures, etc.) in a single file on disk, in the data/ directory of the gitea installation.

The git repository is, similarly, a single file on disk, with the entire database of commits, blogs, commit histories, etc., all contained in the .git directory, which is contained in the repositories directory of the gitea installation.

That means backing up your git server is as easy as copying the gitea folder. No need to back up a MySQL database or do a funny pants dance to export your database to a proprietary format.

This is another central tenent of git's design philosophy - be fast, pack light, and travel easily.

How Gitea Fits Into Git Patterns

There are many resources on git, and some cover the concept of "git patterns," or templates for how to use git.

Because git is designed to be decentralized, gitea provides a "centralized" node for collaboration within a decentralized system. So you could use gitea to collaborate with your local Team A, and push and pull branches and work on various features together. Then, once Team A has put together a branch they've found useful, they can push it to a different remote server that is more widely accessed.

(Note that this is the logic behind why you need to check out all the branches and tags, locally, that you want to push to the gitea remote server - this allows you the flexibility to only share select branches, so that you might have some branches shared in common wth gitea and github, and other branches only existing on gitea.)

Team B and Team C may use github, and not gitea, to access the project code. The gitea server may for example be a private server on a local network, whereas github is better suited for collaboration. By pushing select branches from the Team A git server, gitea, to the github server, Team B and Team C will then be able to access them from github.

You could also have multiple gitea/gitlab/github enterprise servers for multiple organizations running on git, and they could share a code base by sharing git repositories, commit histories, branches, and so on.

Wrapup

Have a look at the Gitea project, the Go language, git, Github for all the nice software that made this possible.

Then have a look at the finished product at git.charlesreid1.com.

Gitea allows you to create organizations, useful for organizing repos related to particular functionality or platforms. For example, rpi is an organization that owns repositories with scripts and software for raspberry pis, docker is an organization that owns repositories with Dockerfiles, and mac holds Mac-related things.

This organization allows better organization of project code - a dotfiles repository that works for a Mac laptop or a Unix server is not necessarily good for a Raspberry Pi or a Docker container, so code is organized accordingly.

Organizations can also be used to organize project-level code. This git repo is in its beginning phases, but has great potential as a great tool that makes git even more functional and provides one more reason to switch to git.

• Before We Begin: The Code
• Timing Scripts
• Before You Time: Developing Your Algorithm
• Beginning Your Timing Journey
• Statistical Timing, a.k.a., If You Give A Mouse A Cookie
• Hierarchical Timing Strategy
• Single Problem/Program/Binary
• Multiple Problem/Program/Binary
• Statistical Averaging
• Results
• Summary

Before We Begin: The Code

Note that all of the code discussed/shown in this post is available from the traveling salesperson problem repository on git.charlesreid1.com. The guava/ directory contains the guava solution to the traveling salesperson problem, along with the timing scripts discussed below, and several example output files.

Introduction

Timing a piece of code can be tricky.

Choosing a random problem of a given size can be problematic, if you happen to randomly chose a particularly easy or difficult case. This can lead to an inaccurate picture of scale-up behavior. Timing results should be statistically averaged - the figure below shows scale-up behavior for the traveling salesperson problem when solving a single random problem, versus a hundred random problems.

This post will cover some conceptual and code tools for measuring the timing and performance of code.

Timing Scripts

Timing a piece of code is a task that sounds simple, on its face. However, the task of profiling code quickly balloons from a single timing of a single bit of code to running hundreds of cases, juggling output from each run, and stitching together script upon script. Soon you find yourself swimming in a pool of output files, looking for your scripts...

In this post we'll cover a workflow for timing a piece of Java code that will help give you a method for thinking about timing. This also balances the need for practicality (i.e., just get it done in as simple a manner as possible) with good design (i.e., flexible inputs and the use of scripts).

Before You Time: Developing Your Algorithm

As you develop your algorithm, you may have variable values hard-coded and random number generators seeding from the same value each time. The intention, as you are developing, is to work out the bugs without the additional difficulty of solving a different problem each time you run the program.

Beginning Your Timing Journey

Once you've implemented your algorithm and verified that it works, the timing portion begins. You can time the code using mechanisms built into the language, which is the most accurate way of timing code. This is called instrumenting your code. To begin with, you might try timing a single problem size, but this information is hard to interpret without more data, so you start to time the code on problems of other sizes.

Here there be dragons.

Statistical Timing, a.k.a., If You Give A Mouse A Cookie

See If You Give A Mouse A Cookie.

Once you time the code solving a single problem, you will want to time the code solving multiple problems.

Once you time the code solving multiple problems, you will want to time the code solving each problem multiple times to get an accurate statistical picture of the solution time on a variety of problems.

Once you get statistics about multiple problem times, you will want to gather statics about variations in problem types and algorithm variations.

It simply does not end. A strategy for managing this deluge of new timing needs prevents spaghetti code.

Hierarchical Timing Strategy

The strategy here is to design code and scripts that are hierarchical. The levels of the hierarchy consist of the different scopes involved in timing: * Single problem/program/binary * Multiple problem/program/binary * Statistical averages using case matrix * Design of Computer Experiments: Testing Variations * Strong and weak scaling (if we decide to continue with parallelization of algorithm)

At each stage, we utilize scripts to bundle the task into a single command or script.

Single Problem/Program/Binary: Makefile

At the scale of solving a single problem, we need a tool that will compile and run Java code - even if it only happens once. Makefiles are an excellent tool for stringing together commands with flags (in the case of the traveling salesperson problem, we need to link to the Guava Jars when we compile and run).

By defining some variables at the top of the Makefile, and a few rules, we have a functional and easy way to build code with scalable complexity:

# Set path to guava
HOME=/Users/charles
GUAVA=$(HOME)/codes/guava/jars/guava-21.0.jar

# Set compile target
BIN=TSP
TARGET=$(BIN).java

# Set java class path
# Hard to believe this actually works, but ok:
CP=-cp '.:$(GUAVA)'


build:
    javac $(CP) $(TARGET) 

run:
    # If no size, use default
    java $(CP) $(BIN) 

time:
    # Java times itself, we just have to pass it the size
    java $(CP) $(BIN) $(SIZE) 

clean:
    rm -rf *.class

Link to code on git.charlesreid1.com

This enables us to run

$ make build 
/Users/charles/codes/guava/jars/guava-21.0.jar

and have a new version of the code compile. We can also run a problem with a default size of 5 nodes with a simple make run command:

$ make run
java -cp '.:/Users/charles/codes/guava/jars/guava-21.0.jar' TSP
------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 2, 3, 4, 1]  Distance: 258
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 2, 3, 1, 4]  Distance: 257
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 2, 4, 1, 3]  Distance: 189
Found solution...?
Elapsed time 0.005529 s

and have the compiled code run. We can also feed arguments to make commands, and have them passed to the command that is executed:

$ make time SIZE=10
# Java times itself, we just have to pass it the size
java -cp '.:/Users/charles/codes/guava/jars/guava-21.0.jar' TSP 10
------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 9, 7, 2, 8, 1, 4]   Distance: 446
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 9, 7, 2, 8, 4, 1]   Distance: 395
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 9, 7, 4, 1, 8, 2]   Distance: 382
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 9, 1, 4, 7, 2, 8]   Distance: 365
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 9, 1, 4, 7, 8, 2]   Distance: 326
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 2, 8, 7, 4, 1, 9]   Distance: 303
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 3, 2, 8, 4, 7, 9, 1]   Distance: 298
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 4, 7, 3, 2, 8, 9, 1]   Distance: 286
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 6, 5, 8, 2, 3, 7, 4, 1, 9]   Distance: 283
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 9, 1, 4, 7, 3, 6, 5, 8, 2]   Distance: 275
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 3, 2, 8, 5, 6, 4, 7, 9, 1]   Distance: 274
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 2, 8, 7, 4, 1, 9, 5, 6, 3]   Distance: 262
!!!!!YAY!!!!!!  NEW SOLUTION    Route: [0, 2, 8, 4, 7, 3, 6, 5, 9, 1]   Distance: 256
Found solution...?
Elapsed time 0.050795 s

For running single cases and gathering small amounts of (initial) timing data, Makefiles greatly simplify the workflow.

Multiple Program/Problem/Binary: Bash

Bash is a faithful scripting language that makes it easy to do simple mechanical tasks like run commands in for loops, necessary for the next level of complexity in our timing hierarchy.

While the task at hand is simple enough, and we could easily use Makefiles, we'll use a separate Bash script for separate functionality and keep things from getting overly complicated in the Makefile.

The essence of the timing script is combining the make time command, which takes a size parameter, with bash for loops.

Here is a stripped down version of the timing script:

make build 

for N in 4 5 6 7 8
do
    make time SIZE=${N} 
done

That's it... The rest is just printing!

The make time command passes the size argument on the command line. The Java Traveling Salesperson Problem code checks if there is an input argument on the command line, and if there is it uses that as the problem size.

Here's a more embellished script:

export RIGHTNOW="`date +"%Y%m%d_%H%M%S"`"
export OUT="timeout_tsp_java_${RIGHTNOW}.out"
touch ${OUT}
cat /dev/null > ${OUT}

# Compile
make build 

for N in {4..8..1}
do
    echo "**************************************" >> ${OUT}
    echo "Running TSP with $N nodes with Java..." >> ${OUT}

    make time SIZE=${N} >> ${OUT} 2>&1

    make dot
    mv graphviz.png graphviz_tsp_${N}.png

    echo "Done." >> ${OUT}

    echo "" >> ${OUT}

done

echo ""
echo ${OUTFILE}
echo ""

Link to code on git.charlesreid1.com

This creates a time-and-date-stamped output file in which all of the output of this script goes - and which can be parsed for plotting the results of timing studies.

Before it times the solution to the TSP, it dumps out a graphviz dot file containing a schematic of the graph that can be diagrammed:

**************************************
Running TSP with 4 nodes with Java...
Found solution.
Elapsed time 0.004679 s
 Done.

**************************************
Running TSP with 5 nodes with Java...
Found solution.
Elapsed time 0.004543 s
 Done.

**************************************
Running TSP with 6 nodes with Java...
Found solution.
Elapsed time 0.006911 s
 Done.

**************************************
Running TSP with 7 nodes with Java...
Found solution.
Elapsed time 0.008286 s
 Done.

**************************************
Running TSP with 8 nodes with Java...
Found solution.
Elapsed time 0.014499 s
 Done.

In this way we can run a quick test matrix of different problem sizes, and see how the code scales.

Statistical Averaging

Of course, any good computational physicist will tell you that scaling behavior extrapolated from running a single case of a single problem size is folly - your random choice of graph could have been an unusually easy or difficult graph, throwing off the results of the timing.

A proper scaling study really needs to take into account the statistical trends in solution time on a random assortment of problems, so we need a way of scripting solutions to dozens or hundreds of random problems and computing statistically representative measures of code performance.

Our code implements a function to generate random graphs, but for testing and debugging purposes the random number generator was seeded with the same value each time. By making the random number generators truly random, each problem we solve will be a different random graph with the specified number ofn odes.

We can accomplish all of this using bash again: within the for loop over different problem sizes, we will add a for loop for repetitions. Here is the basic framework:

make build 

for N in {4..10..1}
do
    for repetition in {0..100..1}
    do
        make time SIZE=${N} 
    done
done

And the embellished version that prints the resulting timing information to a file:

# Compile
make build 

export RIGHTNOW="`date +"%Y%m%d_%H%M%S"`"

for N in {4..10..1}
do

    export OUT="avgtimeout_tsp_${RIGHTNOW}_${N}.out"
    touch ${OUT}

    echo "**************************************" >> ${OUT}
    echo "Running TSP with $N nodes with Java..." >> ${OUT}

    for repetition in {0..100..1}
    do
        make time SIZE=${N} >> ${OUT} 2>&1
    done
    echo "Done." >> ${OUT}
    echo "" >> ${OUT}

done

echo ""
echo ${OUTFILE}
echo ""

Link to code on git.charlesreid1.com

This results in a file with a large amount of information, but it can be trimmed down to the quantities of interest using a little command line fu. Here are filtered results from an 11-node traveling salesperson problem run approximately 102 times:

$ cat avgtimeout_tsp_20170330_235134_11.out | grep Elapsed | wc -l
     102

$ cat avgtimeout_tsp_20170330_235134_11.out | grep Elapsed
Elapsed time 0.082839 s
Elapsed time 0.130378 s
Elapsed time 0.173737 s
Elapsed time 0.100067 s
Elapsed time 0.166046 s

<clipped>

Elapsed time 0.147801 s
Elapsed time 0.285777 s
Elapsed time 0.078655 s
Elapsed time 0.081246 s
Elapsed time 0.174288 s

Now we have a Makefile that allows us to build and run with a single command, and a bash script that loops over each problem size and runs a set of computations for each problem size. But how to compute an average?

We have an assortment of choices - Python being the most obvious - but in the spirit of old-school Unix tools like make, cat, grep, and wc, let's use awk to compute the average walltime for each case size.

Awk to Compute Average Walltime

Given the following output of elapsed walltime for different problem sizes,

$ cat avgtimeout_tsp_20170330_235134_11.out | grep Elapsed
Elapsed time 0.082839 s
Elapsed time 0.130378 s
Elapsed time 0.173737 s
Elapsed time 0.100067 s
Elapsed time 0.166046 s

<clipped>

Elapsed time 0.147801 s
Elapsed time 0.285777 s
Elapsed time 0.078655 s
Elapsed time 0.081246 s
Elapsed time 0.174288 s

we want to extract two things: the first is the problem size (contained in the filename), and the second is the column of numbers.

We can extract the problem size from the filename using sed, by searching for the pattern _8.out or _10.out. Here is a Bash one-liner that does this for a variable $f containing the filename:

    N=$(echo $f | sed 's/^.*_\([0-9]\{1,\}\).out/\1/')

The next thing we wnat to do is extract the column of timing data. This is a good task for the cut utility. We can pass it two flags, -d to tell it what to use as a field delimiter, and -f to tell it which field (column) to return. To extract the third column,

    cat $f | grep "Elapsed" | cut -d" " -f3 

This command results in a series of floating point numbers. If we can pipe it to a program that can do simple math, like awk, we can compute an average (which is pretty simple math).

Since awk is a text-proecssing program that happens to be able to interpret numbers as numbers, we have to think like a text processing program. To compute an average, we accumulate the sum of each line in the file, using an accumulator variable. When we have gone through each line in the file, we divide this cumulative sum by the number of lines in the file.

    cat $f | grep "Elapsed" | cut -d" " -f3 | awk '{a+=$1} END{print a/NR}'

This one-liner uses two important concepts in awk, the first is the bracketed blocks {} some denoted with BEGIN and END, and the second is the set of built-in variables available in awk.

By surrounding statements by brackets, we denote a block of statements to be run together as the main body of the program. If the bracket is prefixed by BEFORE, this block of statements is run once at the beginning of the program. If the bracket is prefixed by END, this block of statements is run once at the end of the program. To compute an average, the main body of the program is to accumulate a cumulative sum variable. The END block, run once at the end, is to divide this cumulative sum by the total number of lines.

Finally, these values can be assigned to Bash variables using $(cmd) syntax:

    export N=$(echo $f | sed 's/^.*_\([0-9]\{1,\}\).out/\1/')
    export AVG=$(cat $f | grep "Elapsed" | cut -d" " -f3 | awk '{a+=$1} END{print a/NR}') 
    echo "Average time : ${N}-node TSP problem : ${AVG} s"

Here is the final script, which loops over all of the output files generated by the statistical average timing script, which runs 10-100 cases per problem size:

#!/bin/sh

for f in `/bin/ls -1 avgtimeout_tsp*`
do
    touch tmpfile 
    cat /dev/null > tmpfile

    export N=$(echo $f | sed 's/^.*_\([0-9]\{1,\}\).out/\1/')
    export AVG=$(cat $f | grep "Elapsed" | cut -d" " -f3 | awk '{a+=$1} END{print a/NR}') 
    echo "Average time : ${N}-node TSP problem : ${AVG} s"

    rm tmpfile
done

Link to code on git.charlesreid1.com

Example output:

$ ./avg_calcs.sh  | sort
Average time : 10-node TSP problem : 0.0492826 s
Average time : 11-node TSP problem : 0.125827 s
Average time : 12-node TSP problem : 0.272998 s
Average time : 13-node TSP problem : 0.56743 s
Average time : 14-node TSP problem : 1.24297 s
Average time : 14-node TSP problem : 1.66563 s
Average time : 15-node TSP problem : 8.08373 s
Average time : 16-node TSP problem : 16.4353 s
Average time : 17-node TSP problem : 94.7363 s
Average time : 18-node TSP problem : 749.798 s
Average time : 4-node TSP problem : 0.00473154 s
Average time : 4-node TSP problem : 0.00475648 s
Average time : 5-node TSP problem : 0.005247 s
Average time : 5-node TSP problem : 0.005765 s
Average time : 6-node TSP problem : 0.00694926 s
Average time : 7-node TSP problem : 0.0100795 s
Average time : 8-node TSP problem : 0.0167346 s
Average time : 9-node TSP problem : 0.028239 s

Inspecting the output from particular solutions of particular random graphs shows a wide variation in the number of shortest paths found. For example, for random graphs consisting of 11 nodes, here are some sample solutions. Note the difference in solution times:

------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 7, 6, 10, 3]   Distance: 597
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 7, 6, 3, 10]   Distance: 582
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 7, 10, 3, 6]   Distance: 560
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 7, 3, 6, 10]   Distance: 553
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 10, 3, 7, 6]   Distance: 540
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 10, 7, 6, 3]   Distance: 532
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 10, 7, 3, 6]   Distance: 503
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 5, 6, 3, 7, 10]   Distance: 498
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 10, 3, 7, 5, 6]   Distance: 450
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 10, 5, 7, 3, 6]   Distance: 440
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 10, 5, 6, 7, 3]   Distance: 422
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 6, 5, 10, 3, 7]   Distance: 421
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 4, 6, 5, 10, 7, 3]   Distance: 380
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 7, 10, 5, 6, 4, 3]   Distance: 364
NEW SOLUTION    Route: [0, 9, 2, 1, 8, 7, 3, 4, 6, 5, 10]   Distance: 357
NEW SOLUTION    Route: [0, 9, 2, 1, 5, 10, 7, 3, 8, 4, 6]   Distance: 352
NEW SOLUTION    Route: [0, 9, 2, 1, 5, 10, 7, 8, 3, 4, 6]   Distance: 336
NEW SOLUTION    Route: [0, 9, 2, 1, 5, 6, 4, 10, 7, 8, 3]   Distance: 330
NEW SOLUTION    Route: [0, 9, 2, 1, 4, 8, 7, 3, 6, 5, 10]   Distance: 326
NEW SOLUTION    Route: [0, 9, 2, 1, 4, 8, 3, 7, 6, 5, 10]   Distance: 320
NEW SOLUTION    Route: [0, 9, 2, 1, 4, 8, 3, 7, 10, 5, 6]   Distance: 298
NEW SOLUTION    Route: [0, 9, 2, 1, 4, 6, 5, 10, 7, 8, 3]   Distance: 261
NEW SOLUTION    Route: [0, 9, 2, 7, 8, 3, 1, 4, 6, 5, 10]   Distance: 250
NEW SOLUTION    Route: [0, 9, 8, 7, 2, 3, 1, 4, 6, 5, 10]   Distance: 245
Found solution.
Elapsed time 0.057047 s

------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 5, 2, 7, 3]   Distance: 650
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 5, 2, 3, 7]   Distance: 641
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 5, 7, 2, 3]   Distance: 638
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 5, 7, 3, 2]   Distance: 630
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 7, 5, 2, 3]   Distance: 589
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 2, 3, 7, 5]   Distance: 580
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 10, 2, 5, 7, 3]   Distance: 548
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 2, 5, 7, 3, 10]   Distance: 533
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 7, 5, 2, 3, 10]   Distance: 522
NEW SOLUTION    Route: [0, 8, 1, 6, 4, 9, 7, 5, 2, 10, 3]   Distance: 495
NEW SOLUTION    Route: [0, 8, 1, 6, 7, 9, 4, 5, 2, 10, 3]   Distance: 494
NEW SOLUTION    Route: [0, 8, 1, 6, 7, 5, 4, 9, 2, 10, 3]   Distance: 493
NEW SOLUTION    Route: [0, 8, 1, 6, 3, 10, 2, 5, 7, 9, 4]   Distance: 490
NEW SOLUTION    Route: [0, 8, 1, 6, 3, 10, 2, 5, 7, 4, 9]   Distance: 486
NEW SOLUTION    Route: [0, 8, 1, 6, 9, 4, 7, 5, 2, 10, 3]   Distance: 467
NEW SOLUTION    Route: [0, 8, 1, 10, 2, 5, 7, 4, 9, 6, 3]   Distance: 453
NEW SOLUTION    Route: [0, 8, 1, 2, 5, 7, 4, 9, 6, 3, 10]   Distance: 442
NEW SOLUTION    Route: [0, 8, 1, 2, 5, 7, 4, 9, 6, 10, 3]   Distance: 437
NEW SOLUTION    Route: [0, 8, 1, 5, 7, 4, 9, 2, 10, 6, 3]   Distance: 433
NEW SOLUTION    Route: [0, 8, 10, 2, 1, 5, 4, 9, 7, 6, 3]   Distance: 427
NEW SOLUTION    Route: [0, 8, 10, 2, 1, 5, 7, 4, 9, 6, 3]   Distance: 400
NEW SOLUTION    Route: [0, 8, 2, 1, 5, 7, 4, 9, 6, 10, 3]   Distance: 399
NEW SOLUTION    Route: [0, 3, 7, 4, 9, 6, 10, 2, 1, 5, 8]   Distance: 394
NEW SOLUTION    Route: [0, 3, 7, 4, 9, 6, 10, 2, 8, 5, 1]   Distance: 389
NEW SOLUTION    Route: [0, 3, 6, 9, 4, 7, 5, 8, 1, 2, 10]   Distance: 384
NEW SOLUTION    Route: [0, 3, 6, 9, 4, 7, 5, 8, 10, 2, 1]   Distance: 382
NEW SOLUTION    Route: [0, 3, 6, 9, 4, 7, 5, 1, 2, 8, 10]   Distance: 374
NEW SOLUTION    Route: [0, 9, 4, 5, 1, 2, 8, 10, 3, 6, 7]   Distance: 373
NEW SOLUTION    Route: [0, 9, 4, 7, 3, 6, 10, 8, 5, 1, 2]   Distance: 365
NEW SOLUTION    Route: [0, 9, 4, 7, 3, 6, 10, 2, 1, 5, 8]   Distance: 360
NEW SOLUTION    Route: [0, 9, 4, 7, 3, 6, 10, 2, 8, 5, 1]   Distance: 355
NEW SOLUTION    Route: [0, 9, 4, 7, 5, 8, 1, 2, 10, 6, 3]   Distance: 345
NEW SOLUTION    Route: [0, 9, 4, 7, 5, 1, 2, 8, 10, 6, 3]   Distance: 335
Found solution.
Elapsed time 0.159882 s

------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 4, 7, 8, 1, 9, 6]   Distance: 500
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 4, 7, 8, 1, 6, 9]   Distance: 498
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 4, 7, 8, 6, 1, 9]   Distance: 493
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 4, 7, 8, 6, 9, 1]   Distance: 481
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 4, 7, 8, 9, 1, 6]   Distance: 443
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 4, 7, 8, 9, 6, 1]   Distance: 429
NEW SOLUTION    Route: [0, 3, 10, 2, 5, 6, 1, 9, 8, 7, 4]   Distance: 417
NEW SOLUTION    Route: [0, 3, 10, 2, 6, 5, 4, 7, 8, 9, 1]   Distance: 360
NEW SOLUTION    Route: [0, 3, 10, 2, 1, 9, 6, 5, 4, 7, 8]   Distance: 359
NEW SOLUTION    Route: [0, 3, 10, 4, 5, 6, 2, 1, 9, 7, 8]   Distance: 358
NEW SOLUTION    Route: [0, 3, 10, 4, 5, 6, 2, 1, 9, 8, 7]   Distance: 342
NEW SOLUTION    Route: [0, 3, 10, 4, 5, 6, 9, 8, 7, 2, 1]   Distance: 340
NEW SOLUTION    Route: [0, 3, 10, 4, 7, 8, 9, 1, 2, 6, 5]   Distance: 310
NEW SOLUTION    Route: [0, 3, 7, 8, 9, 10, 4, 5, 6, 2, 1]   Distance: 305
NEW SOLUTION    Route: [0, 3, 9, 8, 7, 4, 10, 1, 2, 6, 5]   Distance: 303
NEW SOLUTION    Route: [0, 5, 4, 7, 3, 10, 8, 9, 6, 2, 1]   Distance: 301
NEW SOLUTION    Route: [0, 5, 4, 7, 3, 10, 1, 2, 6, 9, 8]   Distance: 293
NEW SOLUTION    Route: [0, 5, 4, 7, 3, 1, 6, 2, 10, 9, 8]   Distance: 286
NEW SOLUTION    Route: [0, 5, 4, 7, 3, 1, 2, 6, 9, 10, 8]   Distance: 281
NEW SOLUTION    Route: [0, 5, 4, 7, 3, 1, 2, 6, 10, 9, 8]   Distance: 275
NEW SOLUTION    Route: [0, 5, 4, 7, 8, 9, 6, 2, 1, 3, 10]   Distance: 270
NEW SOLUTION    Route: [0, 5, 4, 7, 8, 9, 10, 3, 1, 2, 6]   Distance: 269
NEW SOLUTION    Route: [0, 5, 4, 10, 3, 7, 8, 9, 6, 2, 1]   Distance: 268
NEW SOLUTION    Route: [0, 5, 4, 10, 9, 8, 7, 3, 1, 2, 6]   Distance: 252
NEW SOLUTION    Route: [0, 5, 4, 10, 9, 6, 2, 1, 3, 7, 8]   Distance: 248
NEW SOLUTION    Route: [0, 5, 6, 2, 10, 4, 7, 8, 9, 3, 1]   Distance: 235
NEW SOLUTION    Route: [0, 5, 6, 2, 1, 3, 10, 4, 7, 8, 9]   Distance: 231
NEW SOLUTION    Route: [0, 5, 6, 2, 1, 3, 7, 4, 10, 9, 8]   Distance: 212
NEW SOLUTION    Route: [0, 5, 6, 2, 1, 3, 9, 10, 4, 7, 8]   Distance: 207
Found solution.
Elapsed time 0.175282 s

------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 10, 4, 9, 3, 8, 1]   Distance: 515
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 10, 4, 9, 3, 1, 8]   Distance: 495
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 10, 4, 9, 8, 1, 3]   Distance: 423
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 10, 4, 8, 9, 1, 3]   Distance: 368
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 10, 4, 3, 8, 9, 1]   Distance: 361
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 10, 4, 3, 1, 9, 8]   Distance: 341
NEW SOLUTION    Route: [0, 6, 7, 2, 5, 1, 9, 8, 3, 4, 10]   Distance: 330
NEW SOLUTION    Route: [0, 6, 7, 2, 10, 5, 1, 9, 8, 4, 3]   Distance: 309
NEW SOLUTION    Route: [0, 6, 7, 10, 2, 5, 1, 9, 8, 4, 3]   Distance: 284
NEW SOLUTION    Route: [0, 6, 7, 8, 9, 1, 5, 2, 10, 4, 3]   Distance: 266
NEW SOLUTION    Route: [0, 6, 7, 8, 9, 1, 5, 10, 2, 4, 3]   Distance: 258
NEW SOLUTION    Route: [0, 6, 5, 2, 10, 4, 3, 1, 9, 8, 7]   Distance: 250
NEW SOLUTION    Route: [0, 6, 5, 2, 10, 7, 8, 9, 1, 3, 4]   Distance: 243
NEW SOLUTION    Route: [0, 6, 5, 2, 4, 3, 1, 9, 8, 7, 10]   Distance: 225
NEW SOLUTION    Route: [0, 6, 5, 1, 9, 8, 7, 10, 2, 4, 3]   Distance: 197
Found solution.
Elapsed time 0.051783 s

------------------- TSP Version 2: The Pessimistic Algorithm ----------------------
NEW SOLUTION    Route: [0, 8, 9, 6, 1, 7, 3, 4, 5, 2, 10]   Distance: 607
NEW SOLUTION    Route: [0, 8, 9, 6, 1, 7, 3, 4, 2, 5, 10]   Distance: 573
NEW SOLUTION    Route: [0, 8, 9, 6, 1, 7, 3, 4, 10, 5, 2]   Distance: 562
NEW SOLUTION    Route: [0, 8, 9, 6, 1, 7, 3, 5, 2, 4, 10]   Distance: 513
NEW SOLUTION    Route: [0, 8, 9, 6, 1, 3, 5, 2, 7, 4, 10]   Distance: 496
NEW SOLUTION    Route: [0, 8, 9, 6, 7, 3, 1, 5, 2, 4, 10]   Distance: 493
NEW SOLUTION    Route: [0, 8, 9, 6, 7, 3, 1, 10, 4, 2, 5]   Distance: 489
NEW SOLUTION    Route: [0, 8, 9, 6, 7, 2, 4, 10, 1, 3, 5]   Distance: 487
NEW SOLUTION    Route: [0, 8, 9, 6, 7, 2, 5, 3, 1, 10, 4]   Distance: 480
NEW SOLUTION    Route: [0, 8, 9, 6, 4, 3, 5, 2, 7, 1, 10]   Distance: 454
NEW SOLUTION    Route: [0, 8, 9, 6, 4, 5, 2, 7, 3, 1, 10]   Distance: 453
NEW SOLUTION    Route: [0, 8, 9, 6, 4, 10, 5, 2, 7, 3, 1]   Distance: 452
NEW SOLUTION    Route: [0, 8, 9, 6, 4, 10, 1, 7, 3, 5, 2]   Distance: 443
NEW SOLUTION    Route: [0, 8, 9, 6, 4, 10, 1, 3, 5, 2, 7]   Distance: 411
NEW SOLUTION    Route: [0, 8, 9, 10, 4, 6, 1, 3, 5, 2, 7]   Distance: 407
NEW SOLUTION    Route: [0, 8, 9, 10, 4, 6, 7, 2, 5, 3, 1]   Distance: 402
NEW SOLUTION    Route: [0, 8, 9, 10, 4, 6, 5, 2, 7, 3, 1]   Distance: 390
NEW SOLUTION    Route: [0, 8, 9, 10, 4, 6, 2, 7, 3, 1, 5]   Distance: 388
NEW SOLUTION    Route: [0, 8, 9, 10, 4, 6, 2, 7, 1, 3, 5]   Distance: 387
NEW SOLUTION    Route: [0, 8, 9, 10, 4, 6, 2, 5, 3, 1, 7]   Distance: 384
NEW SOLUTION    Route: [0, 8, 9, 10, 1, 3, 5, 2, 7, 4, 6]   Distance: 376
NEW SOLUTION    Route: [0, 8, 9, 10, 6, 4, 3, 1, 7, 2, 5]   Distance: 371
NEW SOLUTION    Route: [0, 8, 9, 10, 6, 4, 3, 1, 5, 2, 7]   Distance: 367
NEW SOLUTION    Route: [0, 8, 9, 10, 6, 4, 2, 5, 3, 1, 7]   Distance: 366
NEW SOLUTION    Route: [0, 8, 9, 10, 6, 4, 7, 2, 5, 3, 1]   Distance: 365
NEW SOLUTION    Route: [0, 8, 9, 5, 3, 1, 10, 6, 4, 2, 7]   Distance: 358
NEW SOLUTION    Route: [0, 8, 9, 5, 2, 7, 3, 1, 10, 4, 6]   Distance: 352
NEW SOLUTION    Route: [0, 8, 2, 4, 6, 10, 9, 5, 3, 7, 1]   Distance: 344
NEW SOLUTION    Route: [0, 8, 2, 4, 6, 10, 9, 5, 3, 1, 7]   Distance: 328
NEW SOLUTION    Route: [0, 8, 2, 7, 3, 1, 5, 9, 10, 4, 6]   Distance: 321
NEW SOLUTION    Route: [0, 8, 2, 7, 1, 3, 5, 9, 10, 4, 6]   Distance: 320
NEW SOLUTION    Route: [0, 8, 5, 3, 1, 9, 10, 6, 4, 2, 7]   Distance: 319
NEW SOLUTION    Route: [0, 8, 5, 9, 10, 6, 4, 2, 7, 3, 1]   Distance: 314
NEW SOLUTION    Route: [0, 8, 5, 2, 7, 3, 1, 9, 10, 4, 6]   Distance: 313
NEW SOLUTION    Route: [0, 8, 4, 3, 5, 2, 7, 1, 9, 10, 6]   Distance: 299
NEW SOLUTION    Route: [0, 8, 4, 3, 7, 2, 5, 9, 1, 10, 6]   Distance: 293
NEW SOLUTION    Route: [0, 8, 4, 3, 1, 7, 2, 5, 9, 10, 6]   Distance: 278
NEW SOLUTION    Route: [0, 8, 4, 2, 7, 3, 1, 5, 9, 10, 6]   Distance: 277
NEW SOLUTION    Route: [0, 8, 4, 2, 7, 1, 3, 5, 9, 10, 6]   Distance: 276
NEW SOLUTION    Route: [0, 8, 4, 6, 10, 9, 5, 3, 1, 7, 2]   Distance: 263
NEW SOLUTION    Route: [0, 8, 4, 6, 10, 9, 5, 3, 1, 2, 7]   Distance: 262
NEW SOLUTION    Route: [0, 8, 4, 6, 10, 9, 5, 2, 7, 3, 1]   Distance: 249
NEW SOLUTION    Route: [0, 3, 5, 9, 10, 6, 4, 8, 1, 7, 2]   Distance: 245
NEW SOLUTION    Route: [0, 3, 5, 9, 10, 6, 4, 8, 1, 2, 7]   Distance: 244
NEW SOLUTION    Route: [0, 3, 7, 2, 5, 9, 10, 1, 8, 4, 6]   Distance: 242
NEW SOLUTION    Route: [0, 3, 7, 2, 5, 9, 10, 6, 4, 8, 1]   Distance: 231
NEW SOLUTION    Route: [0, 3, 1, 8, 4, 6, 10, 9, 5, 2, 7]   Distance: 215
Found solution.
Elapsed time 0.087109 s

Results

The figure below shows the results of the timing study when using the average of 100 different random problems, compared to the timing study performed using a single problem size.

The results show dramatically different behavior, highlighting the importance of computing the statistical average of solution walltime for many different problems. This was not an issue that arose in discussing timing or profiling of codes to solve the 8 queens problem, because in that case the problem (and resulting decision tree) were determined by the choice of algorithm.

This information is also important ot keep in mind when comparing the timing performance of two algorithms - using many cases to compare two algorithms is preferrable, since it reduces the likelihood of randomly selecting a problem that highights a weakness of one algorithm or a strength of the other.

Summary

In this post we covered some scripting tools that make timing a lot easier to do, and some ways of thinking about and building up scripts to allow for more complex timing studies without an increase in the associated post-processing work involved.

We showed how to use make and a Makefile to create compact, expressive commands to build and run Java programs. We showed how to use Bash scripting to implement loops and run a case matrix of problems of various sizes, measuring timing data for hundreds of problems in total. All of these scripts made heavy use of Unix command line tools, demonstrating how to chain commands and functionality together on the command line to accomplish complex tasks. Finally, we showed how to use the awk programming language to compute the average of a set of numbers, exploring yet another application of this unusually handy language.

• Intro
• The Graphs We Are Solving
  • Visualizations of Graphs
• Guava TSP Solution
  • Timing the TSP Solution
• Improving the Guava TSP Solution
  • The Flaw
  • Fixing the Flaw
  • The Pessimist Algorithm
• Timing Results
• Future Work

Intro

In a prior blog post we introduced you to the traveling salesperson problem (TSP), which involves finding the shortest path through every city in a group of cities connected by a network of roads. Using Google Guava, we have implemented a solution to the TSP in Java.

Our philosophy toward timing, profiling, and optimization is that it is always best to work from data - and timing is the first place to begin collecting data. As we will show in this blog post, simply timing your function for different problem sizes can reveal scaling behavior that indicates bottlenecks, bugs, or inefficiencies in the algorithm.

In this post, we use simple timing tools and a spreadsheet to plot scaling behavior and identify bottlenecks in the traveling salesperson problem code. Fixing the bottleneck led to a reduction in cost of two orders of magnitude.

Here's a preview:

In this post we'll cover what we did to time the problem, the initial results, and the algorithm improvement that led to the massive performance improvement.

But first, let's look at some of the graphs that are being solved.

The Graphs We Are Solving

Let's start by having a look at some of the graphs we will be solving, and the representation of the problem.

Visualizations of Graphs

The first few graphs start out simple: here is a randomly generated 4-node traveling salesman problem (we wil cover the code that generates the graph pictured here in a moment):

Shortest Route: [0, 2, 3, 1] Distance: 112.0

Here is another randomly generated graph with 5 nodes:

Shortest Route: [0, 4, 2, 1, 3] Distance: 130.0

With 6 nodes:

Shortest Route: [0, 2, 4, 1, 5, 3] Distance: 163.0

But problem of this sise are still trivially easy for a processor to handle. Our inefficient, first-pass algorithm started to show signs of eating up CPU cycles at around 9 nodes (albeit less than 1 second). Here is the graph with 9 nodes:

Shortest Route: [0, 6, 1, 7, 3, 2, 5, 8, 4] Distance: 166.0

With 12 nodes:

Shortest Route: [0, 7, 5, 4, 1, 8, 6, 10, 11, 9, 3, 2] Distance: 236.0

At 14 nodes, even the efficient algorithm crosses the 1 second threshold.

Shortest Route: [0, 2, 6, 10, 13, 12, 7, 4, 1, 11, 5, 3, 9, 8] Distance: 277.0

We tested randomly-generated, fully-connected graphs of up to 18 nodes, and the algorithm was able to compute solutions within a few minutes. Here is an 18-node graph:

Shortest Route: [0, 3, 10, 6, 12, 5, 11, 2, 14, 8, 13, 4, 7, 1, 9] Distance: 267.0

The Guava TSP Solution

In a prior post we covered the implementation of a solution to the TSP using Guava's Network objects. This implementation utilized a recursive depth-first search algorithm to search for the shortest path among all nodes.

To recap, here was our pseudocode for the TSP solution:

explore(neighbors):

    if(no more unvisited neighbors):
        # This is the base case.
        if total distance is less than current minimum:
            save path and new minimum

    else:
        # This is the recursive case.
        for neighbor in unvisited neighbors:
            visit neighbor
            explore(new_neighbors)
            unvisit neighbor

And here is what the recursive backtracking explore() method looked like when implemented in Java:

    /** Recursive backtracking method: explore possible solutions starting at this node, having made nchoices */
    public void explore(Node node, int nchoices) {

        if(nchoices == graphSize) {
            // 
            // BASE CASE
            //
            if(this.this_distance < this.min_distance || this.min_distance < 0) {
                // Solution base case
                this.min_distance = this.this_distance;
                printSolution();
            }

        } else {
            //
            // RECURSIVE CASE
            //  
            Set<Node> neighbors = graph.adjacentNodes(node);
            for(Node neighbor : neighbors) {
                if(neighbor.visited == false) {

                    int distance_btwn = -10000;

                    for( Edge edge : graph.edgesConnecting(node, neighbor) ) {
                        distance_btwn = edge.value;
                    }

                    // Make a choice
                    this.route[nchoices] = neighbor.id;
                    neighbor.visit();
                    this.this_distance += distance_btwn;

                    // Explore the consequences
                    explore(neighbor,nchoices+1);

                    // Unmake the choice
                    this.route[nchoices] = -1;
                    neighbor.unvisit();
                    this.this_distance -= distance_btwn;
                }
                // Move on to the next choice (continue loop)
            }               
        } // End base/recursive case
    }

Note: full TSP code available at http://git.charlesreid1.com/charlesreid1/tsp.

Timing the TSP Solution

To time the Guava solution to the TSP, we utilized Java's system time to measure the amount of time it took to compute solutions, excluding the time spent on graph construction.

Here is the code that performs the timing of the call to the explore method:

    public static void main(String[] args) throws IllegalArgumentException { 

        ...

        double conn = 1.00;
        TSP t = new TSP(N,conn);

        long start = System.nanoTime();
        t.solve();
        long end = System.nanoTime();
        long duration = end - start;

        System.out.printf("Elapsed time %03f s\n ", (duration/1E9) );
    }

The elapsed time is computed using System.nanoTime().

Writing a script to feed variable size graphs and time the resulting code showed some pretty awful scaling behavior:

This scaling behavior reveals a bottleneck in the algorithm: the algorithm scales the same way the problem size scales. A more efficient algorithm would be capable of ruling out more of the solution space as the graph size grows, allowing the algorithm to scale better at large problem sizes.

This led to some reconsideration of the algorithm.

Improving the Guava TSP Solution

The original TSP algorithm implemented a subtle flaw - not by implementing a mistake in the calculation, but by ignoring an important piece of information.

The Flaw

As the recursive depth-first search traverses the graph, the algorithm is checking if all nodes have been traversed. When all nodes have been traversed, it then compares the distance of that journey to the current shortest journey. If the new journey is shorter, it is saved as the new shortest journey, otherwise it is ignored and we move on.

What this ignores is the fact that any path, at any point, can be checked to see if it is longer than the current minimum, and if it is, any possibilities that follow from it can be skipped.

For example, consider the TSP on a graph of six cities, A B C D E F.

Suppose that the algorithm is in the midst of the recursive backtracking solution, and has a current minimum distance and minimum path of the route A-B-E-D-C-F, which is 24 miles.

Now suppose that the algorithm is searching for solutions that begin with the choice A-E-C, and the distance A-E-C is 28 miles.

The naive algorithm ignores this information, and continues choosing from among the 3 remaining cities, computing the total length for \(3! = 6\) additional routes, and finding that all six of them do not work.

The smart algorithm checks each time it chooses a new node whether the length of the current route exceeds the current minimum route distance (if one has been found/set). If not, the algorithm keeps going, but if so, it skips choosing neighbors and returns directly to the parent caller.

Fixing the Flaw

Fixing the flaw is surpsingly easy: we just add an if statement.

Illustrating first with the pseudocode:

explore(neighbors):

    if(no more unvisited neighbors):
        # This is the base case.
        if total distance is less than current minimum:
            save path and new minimum

    else:
        # This is the recursive case.
        if current distance is greater than current minimum:
            skip
        else:
            for neighbor in unvisited neighbors:
                visit neighbor
                explore(new_neighbors)
                unvisit neighbor

In our Java implementation, the algorithm simply prints out solutions as it goes, then returns to the calling function whether a solution was found or not. Thus, we can "skip" a set of solutions by just returning to the calling function, using a return statement.

        if(nchoices == graphSize) {
            // 
            // BASE CASE
            //
            if(this.this_distance < this.min_distance || this.min_distance < 0) {
                // Solution base case:
                this.min_distance = this.this_distance;
                printSolution();
            }

        } else {
            //
            // RECURSIVE CASE
            //  

            /* 
             * The following lines result in a huge computational cost savings.
            */
            if(this.min_distance>0 && this.this_distance>this.min_distance) {
                // Just give up already. It's meaningless. There's no point.
                return;
            }

            // Everything else stays exactly the same
            Set<Node> neighbors = graph.adjacentNodes(node);
            for(Node neighbor : neighbors) {
                if(neighbor.visited == false) {

                    int distance_btwn = -10000;

                    for( Edge edge : graph.edgesConnecting(node, neighbor) ) {
                        distance_btwn = edge.value;
                    }

                    // Make a choice
                    this.route[nchoices] = neighbor.id;
                    neighbor.visit();
                    this.this_distance += distance_btwn;

                    // Explore the consequences
                    explore(neighbor,nchoices+1);

                    // Unmake the choice
                    this.route[nchoices] = -1;
                    neighbor.unvisit();
                    this.this_distance -= distance_btwn;
                }
                // Move on to the next choice (continue loop)
            }               
        } // End base/recursive case
    }

The Pessimist Algorithm

This algorithm is dubbed The Pessimist Algorithm. Let's see how it works. Here is that new if statement:

if(this.min_distance>0 && this.this_distance>this.min_distance) {
    // Just give up already. It's meaningless. There's no point.
    return;
}

This if statement tests two conditions - first, we check if a first minimum distance has actually been found, and second, we check if the distance of the current path is greater than the minimum distance. If it is, we give up continuing our search down this path, and just return back to the calling function.

This introduces a small computational cost - we now have an if statement to check every time the explore() method is called - but it results in such significant cost savings that it does not matter.

Timing Results

Shown below is a graph of the walltime for various problem sizes, showing both the original algorithm and the pessimist algorithm and their scaling behavior.

The pessimist algorithm led to a drastic improvement in scale-up - the results are striking.

And here are the results in a table form:

-----------------------------------------------------------------------------------------
| Number of Nodes N | Initial Algorithm Walltime [s] | Pessimist Algorithm Walltime [s] |
|-------------------|--------------------------------|----------------------------------|
| 4                 | 0.005                          | 0.006                            |
| 5                 | 0.006                          | 0.006                            |
| 6                 | 0.009                          | 0.008                            |
| 7                 | 0.017                          | 0.011                            |
| 8                 | 0.029                          | 0.020                            |
| 9                 | 0.083                          | 0.023                            |
| 10                | 0.305                          | 0.053                            |
| 11                | 1.443                          | 0.118                            |
| 12                | 15.808                         | 0.149                            |
| 13                | 180.078                        | 0.524                            |
| 14                |                                | 1.276                            |
| 15                |                                | 3.905                            |
| 16                |                                | 216.827                          |
| 17                |                                | 106.992                          |
| 18                |                                | 337.930                          |
-----------------------------------------------------------------------------------------

For a problem with 13 nodes, the initial algorithm took 3 minutes; the pessimist algorithm didn't even break the one second mark!

Future Work

Now that we've got the algorithm running faster and more efficiently, we can tackle larger problems and explore the impact of problem topology on solutions, and we can rest assured we have an efficient algorithm that can scale to larger and more interesting problems.

There are further improvements we could make to the algorithm to improve it, though. By examining the solutions that are found, we can see that the solutions usually, but not always, connects from each neighbor to its next-closest neighbor. If, when iterating over neighbors, we start by searching the nearest neighbors first, we can potentially get to the minimum solution faster, which would allow us to more quickly rule out larger portions of the solution space that are infeasible.

This would induce an additional overhead cost of sorting, since the Guava library returns the edges that connect to a node as an unordered Set. These edges would have to be added to a container and sorted to implement the nearest-neighbor search.

However, we saw with the pessimist solution that a small increase in complexity can rule out large enough portions of the solution space to make it worthwhile, so it may be that the cost of sorting each edge pays off in the computational savings that result.